Optimize E-Commerce Last-Mile Delivery with Python

Organize your routes to deliver parcels with a minimum number of drivers using optimization models with python

Article originally published on Medium.

If you travel to first and second-tier cities of China, you will find on the street many delivery drivers (Chinese: 快递).

They take the parcels from small warehouses called customer service centres (Chinese:客户服务中心) located in each neighbourhood and deliver them to the final customers.

These centres are key elements of the Logistics Network of the major courier companies in China.

They provide a large geographical coverage for last-mile delivery and a huge competitive advantage by offering the best service level and delivery lead time in the market.

Before arriving at your door, your parcel will be picked up from the vendor’s warehouse, transit through several regional distribution centres and will finally arrive at the service centre of your neighbourhood.

When your parcel arrives at the centre, you will receive a notification on your phone that a courier will deliver your parcel during the day.

This article will present a solution to optimize the last-mile delivery from these centres to reduce costs and ensure a uniform workload distribution to each driver.

💌 New articles straight in your inbox for free: Newsletter

Scenario

Problem Statement

You are a manager in a local service centre with

• 4 drivers in your team
• 15 parcel capacity per vehicle
• 16 destinations to cover in the neighbourhood named Dj with j in [1, 16]
• D0 is the centre
• 1 route per driver

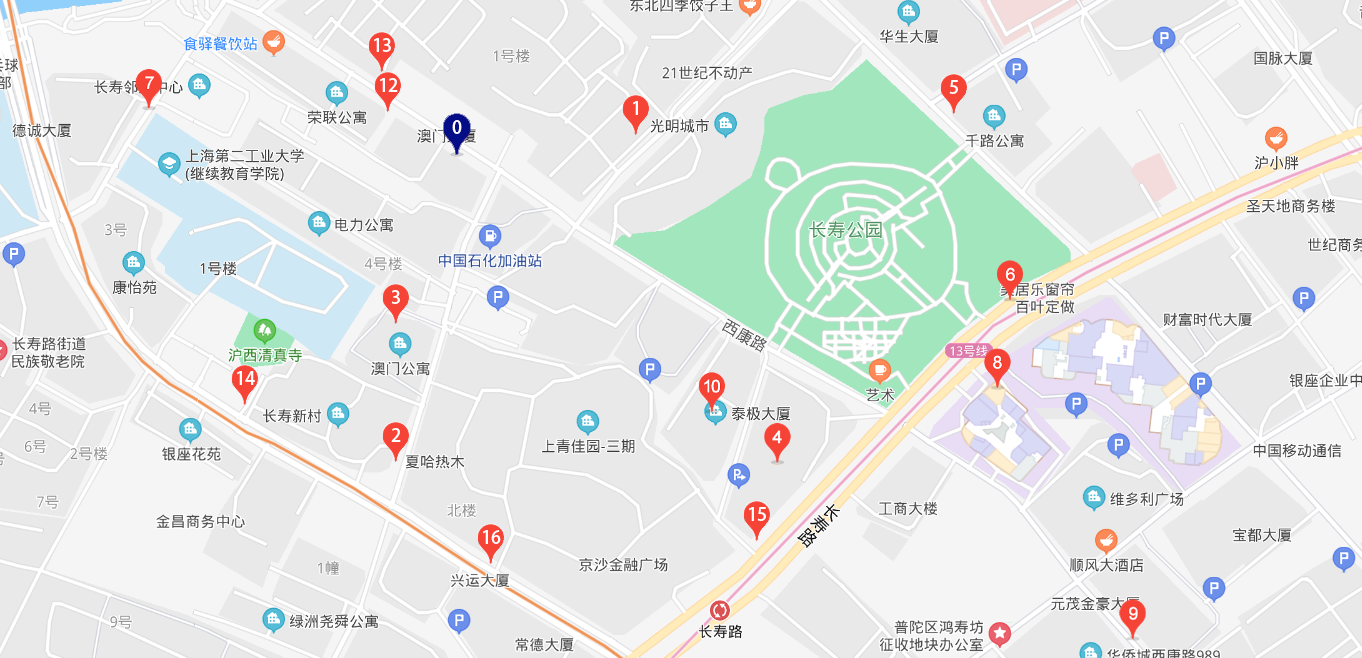
Distance Matrix

To build your model, you need to provide a distance matrix M as inputs defined by

• M(i, j) with i, j in [0, 16]
• M(i, j) = distance between Di and Dj

This distance matrix will be loaded from an Excel file.

Demand: number of parcels to deliver to each location

We will use here a Python list with the first value at zero (because you don’t deliver anything in the centre)

• Demand = [0, 1, 1, 2, 4, 2, 4, 8, 8, 1, 2, 1, 2, 4, 4, 8, 8]

Objective

• Deliver all parcels with a minimum number of drivers
• Optimize the routing to minimize the distance covered per route

Based on these results, you can assign each of your four drivers a route that has the same total distance

• 100% of parcels are delivered with a minimum distance covered
• Drivers’ vehicles are loaded to their maximum capacity (15/15)

Using this model helps you to ensure that your drivers, who are paid a fixed amount by delivery, will be fairly assigned to a route.

You will avoid the issue of having drivers complaining because they have longer routes than their colleagues.

Moreover, you are using your resources at their maximum capacity.

Build your Model

Capacitated vehicle routing problem (CVRP) with Google OR-Tools

OR-Tools is an open-source collection of Google with tools for combinatorial optimization. The objective is to find the best solution out of a very large set of possible solutions.

Let us try to use this library to build the optimal routes.

Import Distance Matrix and Init parameters

Create functions to calculate distances and order quantities

Build your model with constraints

Show the solution

Conclusion

This model can help the centre manager to

• Optimize his fleet with full utilization of his drivers and vehicles
• Ensure that the workload is equally distributed among each driver

Question:

• What could be the results with higher capacity (boxes) per driver?
• What would the results be if we had a weight or volume constraint?

About Me

Let’s connect on Linkedin and Twitter, I am a Supply Chain Engineer that is using data analytics to improve logistics operations and reduce costs.

If you’re looking for tailored consulting solutions to optimize your supply chain and meet sustainability goals, feel free to contact me.