Raw Materials Optimization for Food Manufacturing with Python

Use linear programming to create an optimal recipe for a cheap meal bar that meets specific nutritional requirements

Article originally published on Medium.

Scenario

As an R&D manager of a large food manufacturer, you need to design a recipe for a new cheap and healthy meal bar.

Meal bars must function as a meal rather than just a snack to fill in the cracks.

This is a Linear Programming problem statement with objectives and constraints.

In this article, we will see how to build a model to design this optimal recipe.

💌 New articles straight in your inbox for free: Newsletter

Problem Statement

Scenario

7 ingredients are available

• Meat: Chicken, Beef, Mutton
• Non-Meat: Rice, Corn, Wheat bran, Peanuts

These ingredients have different nutrition facts (in grams) per gram

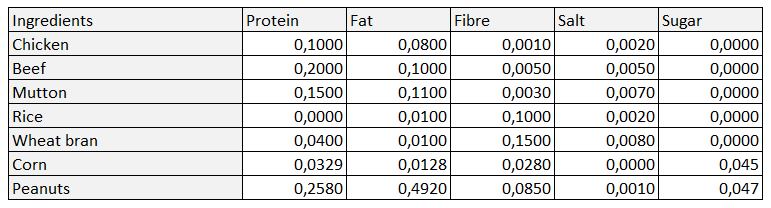
They have also different costs ($/gram)

Objective

Minimize the total cost per bar (Weight: 120g).

Constraints

Minimal values for protein and fibre

• Protein: 20g
• Fibre: 6g

Maximum values for fat, salt and sugar

• Fat: 22g
• Salt: 3g
• Sugar: 30g

Results

• Scenario 1: initial scenario

You only need to put beef, peanuts and wheat bran for a total cost of 7.91$ per bar (120 g).

• Scenario 2: reduce the protein level to 12 g

Your bar is now purely vegan and quite cheap.

• Scenario 3: reduce the sugar to 20 g

To ensure a low level of sugar, you need to use more meat. Therefore you will see your cost per bar increasing.

Build your model

PuLP is a modelling framework for Linear (LP) and Integer Programming (IP) problems written in Python and maintained by COIN-OR Foundation (Computational Infrastructure for Operations Research).

Import Parameters

You can also find these datasets in my GitHub repository.

Nutrition facts

Ingredients Costs

Declare your variables, parameters and model

• LpMinimize: your objective is to minimize the cost of your bar
• lowBound =0: you cannot have a negative value of ingredient quantity

Define the objective and add constraints

Solve your model and analyze the results

Next Steps

This solution is not perfect, you can easily improve it.

• What if your customers want corn?

You can add corn to this recipe by constraining the minimum quantity of corn.

• Do we have infinite possibilities?

Let us try to change the quantity from 120 g to 100 g. What is the result?

For this combination of constraints, there is no optimal solution for a bar of 100g.

To get the minimum quantity, start by listing the constraints (nutrition facts) and then try to find the feasible minimum quantity.

About Me

Let’s connect on Linkedin and Twitter, I am a Supply Chain Engineer that is using data analytics to improve logistics operations and reduce costs.

If you’re looking for tailored consulting solutions to optimize your supply chain and meet sustainability goals, feel free to contact me.

References

[1] Computational Infrastructure for Operations Research, Optimization with PuLP (Documentation), Link