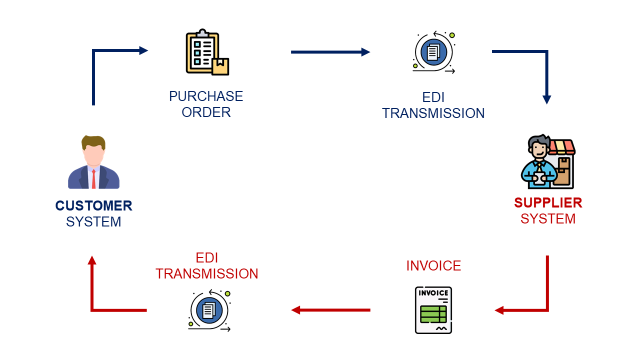
Supply Planning using Linear Programming with Python

Where do you need to allocate your stock to meet customers' demands and reduce your transportation costs?

Article originally published on Medium.

Supply planning is the process of managing the inventory produced by manufacturing to fulfil the requirements created from the demand plan.

Your target is to balance supply and demand in a manner to ensure the best service level at the lowest cost.

In this article, we will present a simple methodology to use Integer Linear Programming to answer a complex Supply Planning Problem considering:

• Inbound Transportation Costs from the Plants to the Distribution Centers (DC) ($/Carton)
• Outbound Transportation Costs from the DCs to the final customer ($/Carton)
• Customer Demand (Carton)

💌 New articles straight in your inbox for free: Newsletter

Scenario

Problem Statement

As a Supply Planning manager of a mid-size manufacturing company, you received feedback that the distribution costs are too high.

Based on the analysis of the Transportation Manager, this is mainly due to the stock allocation rules.

In some cases, your customers are not shipped by the closest distribution centre, which impacts your freight costs.

Your Distribution Network

• 2 plants producing products with infinite capacity
  Note: we’ll see later how we can improve this assumption easily
• 2 distribution centres that receive finished goods from the two plants and deliver them to the final customers
  Note: we will consider that these warehouses operate X-Docking to avoid considering the concept of stock capacity in our model
• 200 stores (delivery points)

To simplify the comprehension, let’s introduce some notations

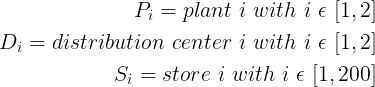
Store Demand
What is the demand per store?

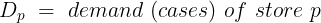
You can download the dataset here.

Transportation Costs

Our main goal is to reduce the total transportation costs, including inbound shipments (from the plants to the DCs) and outbound shipments (from the DCS to the stores).

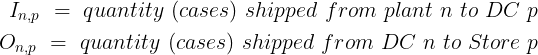
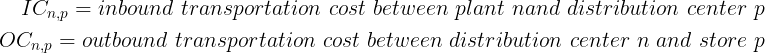
Question

Which Plant i and Distribution n should I chose to produce and deliver 100 units to Store p at the lowest cost?

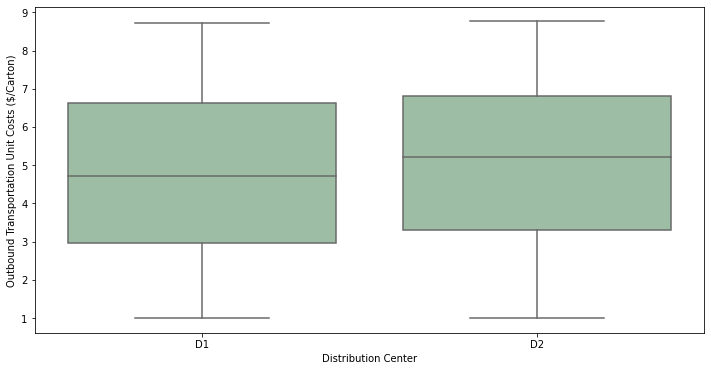
Comment

We can see on the box plot above that the D1 distribution of Unit Cost has a median value lower than D2. We can expect that the model will direct a major part of the flow through D1.

Build your Model

We will be using the PuLP library of python.

PuLP is a modelling framework for Linear (LP) and Integer Programming (IP) problems written in Python and maintained by COIN-OR Foundation (Computational Infrastructure for Operations Research).

Declare your decision variables

What are you trying to decide?

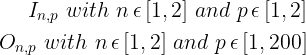
We want to decide the quantity of Inbound and Outbound transportation.

Declare your objective function

What do you want to minimize?

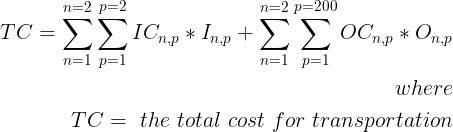
We want to decide to minimize the inbound and outbound transportation costs.

Define the constraints

What are the limits in resources that will determine your feasible region?

The Supply from DCs needs to meet the demand per store.

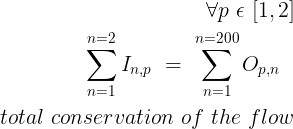
We don’t build any stock in the X-Docking platforms.

Solve the model and prepare the results

What are the results of your simulation?

Result

The model takes the cheapest route for Inbound by linking P2 with D1 (resp. P1 with D2).

As we expected, more than 90% of the outbound flow goes through D1 to minimize outbound costs to minimize Outbound Costs.

Conclusion & Next Steps

Conclusion

This methodology allows you to perform large-scale optimization by implementing simple rules. You will normally avoid having a store not delivered by the most optimal route possible.

Next Steps

The model presented here can be easily improved by adding operational constraints:

• Production Costs in Plants ($/Case)
• Maximal X-Docking Capacity in Distribution Centers (Cartons)

But also by improving the cost structure by adding

• Fixed/Variable Costs Structures in Distribution Centers ($)
• Fixed + Variable Transportation Costs Structure y = (Ax +b)

The only limit you will find is the linearity of the constraints and the objective functions.

YOU CAN’T

• Implement a non-linear production costs rule = f(Cases) to simulate the economies of scale during the production process.
• Implement a non-linear (by range) transportation costs rule of total shipment size.

As soon as you try to touch the linearity of the objective function or the constraints, you leave the beautiful world of linear programming and face the pain of non-linear optimization.

We will explore an example in the next article, and we’ll try to measure the impact of processing time and algorithm complexity.

About Me

Let’s connect on Linkedin and Twitter, I am a Supply Chain Engineer that is using data analytics to improve logistics operations and reduce costs.

If you’re looking for tailored consulting solutions to optimize your supply chain and meet sustainability goals, please contact me.

References

[1] Computational Infrastructure for Operations Research, Optimization with PuLP (Documentation), Link

If you’re looking for tailored consulting solutions to optimize your supply chain and meet sustainability goals, feel free to contact me.